CO-oxidation in a platinum model.¶

In [Khi90], [BIK78], [Bey94] the following chemical model is considered

\[\begin{split} \begin{cases} \begin{aligned} z &= 1 - x - y - s, \\ \dot x &= 2k_1z^2 - 2k_{-1}x^2 - k_3xy, \\ \dot y &= k_2z - k_{-2}y - k_3xy, \\ \dot s &= k_4(z - \lambda s). \end{aligned} \end{cases} \end{split}\]

The model describes CO-oxidation in platinum. Here \(x, y, z\) and \(s\) are the concentrations with \(x + y + z + s = 1\) and \(k_i\) stand for the reaction rate constants.

Overview¶

In this demo we will revisit and extend the results from [BAH15], using the new homoclinic predictor from [Kuz21]. Thus, we will:

Compute a curve of equilibria, parametrized by \(k_2\).
Detect two limit points (LP).
Start continuation from the limit points in two parameters \((\lambda,k_2)\).
Detect two Bogdanov-Takens points.
Start continuation of the homoclinic bifurcation curve emanating from the Bogdanov-Takens points in two parameters \((\lambda,k_2)\).
Compare the predicted and computed homoclinic bifurcation curve emanating from the first Bogdanov-Takens point in parameters space.
Create a convergence plot comparing the different homoclinic approximations derived in [Kuz21].

Load MatCont¶

Before we can start using MatCont we need to add the main directory of MatCont, as well as various subdirectories of MatCont, to the MATLAB search path. This is done in the code below. The variable matcont_home should point to the main directory of MatCont.

clear all
matcontpath = '../';
addpath(matcontpath)
addpath([matcontpath, 'Equilibrium'])
addpath([matcontpath, 'Systems'])
addpath([matcontpath, 'Hopf'])
addpath([matcontpath, 'Homoclinic'])
addpath([matcontpath, 'LimitPoint'])
addpath([matcontpath, 'LimitCycle'])
addpath([matcontpath, 'Continuer'])
addpath([matcontpath, 'MultilinearForms'])
addpath([matcontpath, 'Utilities'])
set(groot, 'defaultTextInterpreter', 'LaTeX');
set(0,'defaultAxesFontSize',15)
set(groot, 'defaultLineMarkerSize', 20);

Set the odefile¶

Next we set the variable odefile to the system file previously generated by the script CO-oxidationGenSym.ipynb.

odefile=@CO_oxidation;

Define equilibrium¶

We manually define an equilibrium at

(3)¶\[(x,y,s) = (0.00295, 0.76211, 0.1678),\]

with parameter values \(k_1=2.5, k_{-1} = 1, k_3 = 10, k_2 = 0, k_{-2} = 0.1, k_4 = 0.0675\) and \(\lambda = 1\).

To refer to the parameters throughout the script we create a cell array of strings containing the parameter names. This is then converted into a struct. This allows us to refer to the parameters as ind.parametername, similar as done in DDE-BifTool.

parnames = {'k1', 'km1', 'k3', 'k2', 'km2', 'k4', 'lambda'};
cind = [parnames;num2cell(1:length(parnames))];
ind  = struct(cind{:});
p(ind.k1) = 2.5;
p(ind.km1) = 1;
p(ind.k3) = 10;
p(ind.km2) = 0.1;
p(ind.k4) = 0.0675;
p(ind.lambda) = 1;
x  = [0.00295; 0.76211; 0.1678];

Continue equilibrium in parameter \(k_2\)¶

To continue the equilibrium (3) in parameter \(k_2\), we first need to obtain a tangent vector to the curve. This is done by the function init_EP_EP. Then we use the function contset to obain a struct containing a list of options which is passed on to the continuer. By adjusting the values of the fields of the opt struct we set the minimum, initial and maximum step sizes, as well as the direction in which to continue (opt.Backward), i.e. in the direction of the obtained tangent vector v1_pred, or its negative. We also set the maximum number of points to continue and weather or not to detect bifurcation points (opt.Singularities) on the equilibrium curve. For more information about all options available to the MatCont continuer and the continuation process in general, we refer to [DGK+08].

Finally, we continue the curve using the function cont.

[x1_pred, v1_pred] = init_EP_EP(odefile, x, p, ind.k2);
opt = contset;
opt.MinStepsize   = 0.00001;
opt.InitStepsize  = 0.0001;
opt.MaxStepsize   = 0.1;
opt.Backward      = 1;
opt.MaxNumPoints  = 300;
opt.Singularities = 1;
[eqbr_x, ~, eqbr_bif_data] = cont(@equilibrium, x1_pred, v1_pred, opt);

first point found
tangent vector to first point found
label = LP, x = ( 0.014843 0.696880 0.144138 1.201115 )
a=1.931461e+00
Neutral saddle
label = H , x = ( 0.016833 0.679849 0.151659 1.202834 )
Neutral saddle
label = H , x = ( 0.116822 0.318191 0.282493 1.428482 )
label = LP, x = ( 0.117575 0.316719 0.282853 1.428493 )
a=-2.384097e+01
label = H , x = ( 0.916533 -0.174248 0.128858 -12.529060 )
First Lyapunov coefficient = -2.462095e+00

elapsed time  = 0.3 secs
npoints curve = 300

There are two limit points detected (LP), two neutral saddles (H) and one Hopf bifurcation point (H). The array struct eqbr_bif_data contains information about the detected bifurcation points. We use this to extract the index of the detected bifurcation points on the equilibrium curve eqbr_x. The equilibrium curve eqbr_x is just a two dimensional array. Each column consists of a point on the curve. The first three rows contain the point \((x,y,s)\) while the last row contains the parameter \(k_2\).

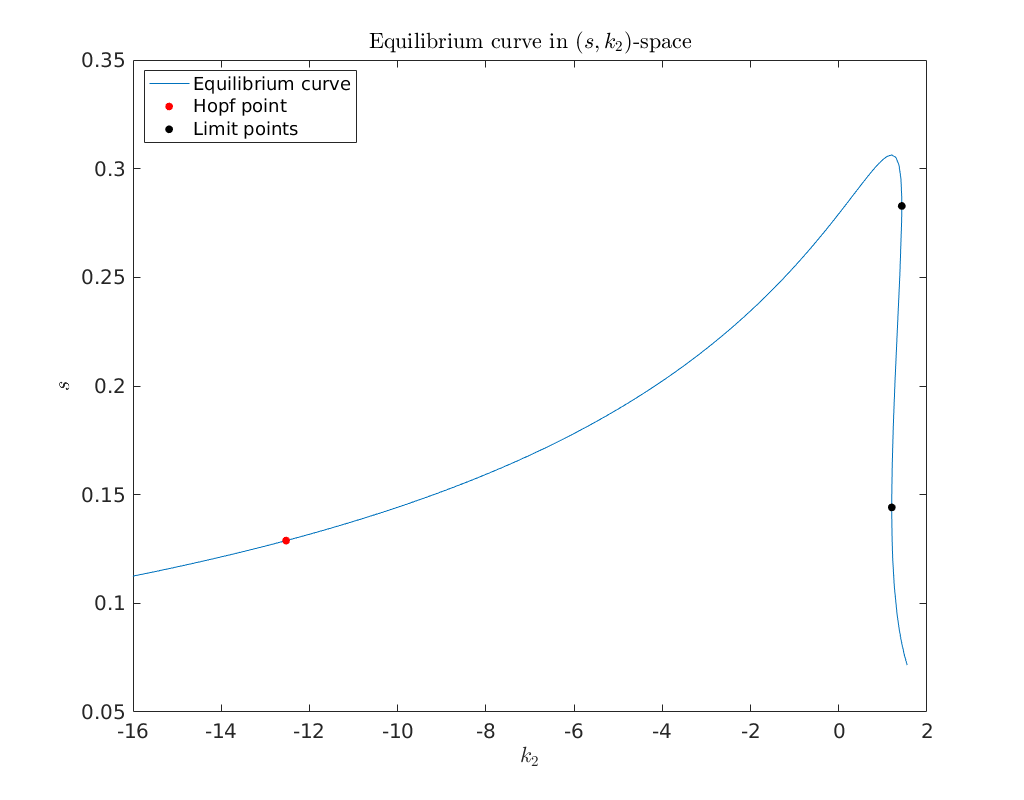
Below we plot the equilibrium curve eqbr_x, together with the detected Hopf and limit points, in \((s,k_2)\)-space.

%plot --width 1024 --height 800
hopfPointInfo   = eqbr_bif_data(strcmp({eqbr_bif_data.msg}, 'Hopf')==1);
limitPointsInfo = eqbr_bif_data(strcmp({eqbr_bif_data.msg}, 'Limit point')==1);
HopfPoint = eqbr_x(:,hopfPointInfo.index);
limitpoint1 = eqbr_x(:,limitPointsInfo(1).index);
limitpoint2 = eqbr_x(:,limitPointsInfo(2).index);
plot(eqbr_x(4,:), eqbr_x(3,:)); hold on
plot(HopfPoint(4), HopfPoint(3), '.r' ,'MarkerSize', 20)
plot(limitpoint1(4), limitpoint1(3),  '.k' ,'MarkerSize', 20)
plot(limitpoint2(4), limitpoint2(3),  '.k' ,'MarkerSize', 20)
xlabel('$k_2$')
ylabel('$s$')
legend({'Equilibrium curve', 'Hopf point', 'Limit points'}, 'Location', 'NorthWest')
title('Equilibrium curve in $(s,k_2)$-space')
axis([-16 2 0.05 0.35])

Construct limit point¶

To continue the first limit point in the parameters \(k_2\) and \(\lambda\) we construct a new point lp containing the position and parameter values. These are needed to obtain an initial tangent vector - using the function init_LP_LP - in the full phase/parameter space. Since, from now on, we will be using the continuation parameter \(k_2\) and \(\lambda\) frequently we assigned these parameters to the variable ap (active parameters).

ap = [ind.k2 ind.lambda]; % continuation parameters
lp1.par = p;
lp1.par(ap) = eqbr_x(4, limitPointsInfo(1).index);
lp1.x = eqbr_x(1:3, limitPointsInfo(1).index);
[x1, v1] = init_LP_LP(odefile, lp1.x, lp1.par', ap);

Continue limit point in parameters \(k\) and \(T_m\)¶

We continue the limit point curve using again the function cont. We use the same continuation options as before defined below in the struct opt, except for the direction of continuation.

opt.Backward = 0;
opt.TestTolerance = 1e-12;
opt.MaxTestIters = 10;
[lp_br1, ~, lp_br1_bif] = cont(@limitpoint, x1, v1, opt);

first point found
tangent vector to first point found
label = BT, x = ( 0.016337 0.638410 0.200456 1.161199 0.722339 )
(a,b)=(-4.822565e-02, -1.937633e+00)
label = CP, x = ( 0.035941 0.352005 0.451370 1.006408 0.355991 )
c=3.627887e-01
label = BT, x = ( 0.115909 0.315467 0.288437 1.417628 0.971398 )
(a,b)=(-8.378444e-02, -2.136280e+00)

elapsed time  = 0.4 secs
npoints curve = 300

There are two Bogdanov-Takens bifurcation points (BT) detected on the limit point branch lp_br1. The second detected Bogdanov-Takens point coincides with the Bogdanov-Takens point teated in [Bey94].

As with the limit points, information about the detected bifurcation points in stored in the struct array lp_br1_bif. Below we extract the Bogdanov-Takens bifurcation points.

bt_points_info = lp_br1_bif(strcmp({lp_br1_bif.label}, 'BT')==1);

Initial prediction of homoclinic orbit near Bogdanov-Takens point 1 (bt1)¶

To obtain an initial approximation to the homoclinic solution near the Bogdanov-Takens point we use the function init_BT_Hom. Its arguments are the system file (odefile), the Bogdanov-Takens point (bt) as defined above, the unfolding parameters (ap) and an options structure (BToptions). The options structure created with the function BT_Hom_set_options contains the following fields:

ntst Number of mesh intervals with a default value of 40.
ncol Number of collocation points used in each interval with a default of 4.
extravec Three dimensional boolean row vector indicating which homoclinic parameters are selected to be free. The first component refers to the half-return time, while the second and third components refer to the distances from the saddle point to the first, respectively, the last point on the homoclinic orbit. The default value is set to [0 1 1]. Thus, the half-return time T is fixed.
order The order of the homoclinic approximation used with a default value of 3.
amplitude Desired amplitude of the homoclinic solution. If left empty then a conservative estimate is made, see [Kuz21].
TTolerance Desired distance between the last point on the homoclinic solution and the saddle point. This should at least be smaller than the amplitude. If left empty it is defined by amplitude*1.0e-03.
HigherOrderTimeReparametrization Boolean to indicate if a higher order approximation to the nonlinear time transformation in the Lindstedt-Poincaré method should be used. This should always be set to 1. It is only implemented for demonstration purposes.
method Selects the method to be used to approximate the homoclinic solution. The different methods available are:
- orbital (the default),
- orbitalv2,
- LP (Lindstedt-Poincaré with smooth normal form),
- LPHypernormalForm,
- RegularPerturbation,
- RegularPerturbationL2.
We refer to [Kuz21] for the interpretations.
messages Boolean to indicate if information about selected parameter should be printed the console. The default value is set to true.
correct Boolean to indicate if the predicted homoclinic solution should be corrected with Newton. The default value is set to true.

Here we will use the default values for the Bogdanov-Takens option structure, except we set the field correct to false and manually correct the approximation.

bt_index = bt_points_info(1).index;
bt1.x = lp_br1(1:3, bt_index);
bt1.par = p';
bt1.par(ap) = lp_br1(4:5, bt_index);
BToptions = BT_Hom_set_options();
BToptions.correct = false;
[x1_pred, v1_pred] = init_BT_Hom(odefile, bt1, ap, BToptions);

Center manifold coefficients' accuracy: 5.023537e-11
BT normal form coefficients:
a=-4.822565e-02,	 b=-1.937633e+00
The initial perturbation parameter epsilon:  1.000000e-01
The initial amplitude: 0.000770702
The initial half-return time T: 1661.8
The initial distance eps0: 4.36004e-07
The initial distance eps1: 1.41437e-06

Correct initial prediction of homoclinic orbit near bt1 with Newton¶

Now that we have an initial prediction for the homoclinic orbit we manually correct it with Newton. After the homoclinic predictor is corrected with the MatCont function newtcorr we use the function bt_rearr (Bogdanov-Takens rearrange) to extract the homoclinic orbit and saddle point from the homoclinic correction.

[hom1_x, hom1_v, ~] = newtcorr(x1_pred, v1_pred);
[x1_orbit, x1_saddle] = bt_rearr(hom1_x);

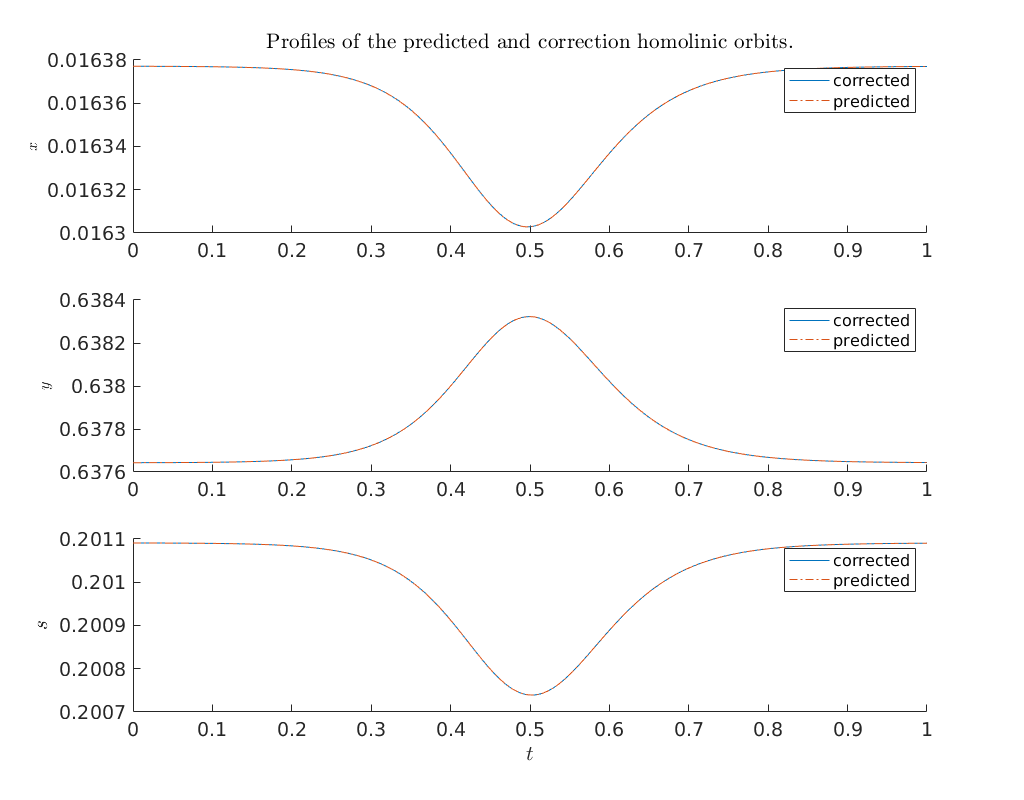
Compare profiles of predicted and corrected solution (bt1)¶

Using again the MatCont function bt_rearr, but now on the homoclinic prediction x1_pred we compare the profiles of the predicted and corrected homoclinic orbits. We see that they are indistinguishable.

global homds
[homoclinic1_pred, saddle1_pred] = bt_rearr(x1_pred);
subplot(3,1,1); hold on;
title('Profiles of the predicted and correction homolinic orbits.')
plot(homds.finemsh, x1_orbit(1:3:end))
plot(homds.finemsh, homoclinic1_pred(1:3:end),'-.')
legend({'corrected', 'predicted'})
ylabel('$x$', 'fontsize', 12,'interpreter', 'latex')
subplot(3,1,2); hold on;
plot(homds.finemsh, x1_orbit(2:3:end))
plot(homds.finemsh, homoclinic1_pred(2:3:end),'-.')
legend({'corrected','predicted'})
ylabel('$y$', 'fontsize', 12,'interpreter', 'latex')
subplot(3,1,3); hold on;
plot(homds.finemsh, x1_orbit(3:3:end))
plot(homds.finemsh, homoclinic1_pred(3:3:end),'-.')
legend({'corrected',  'predicted'})
xlabel('$t$')
ylabel('$s$')

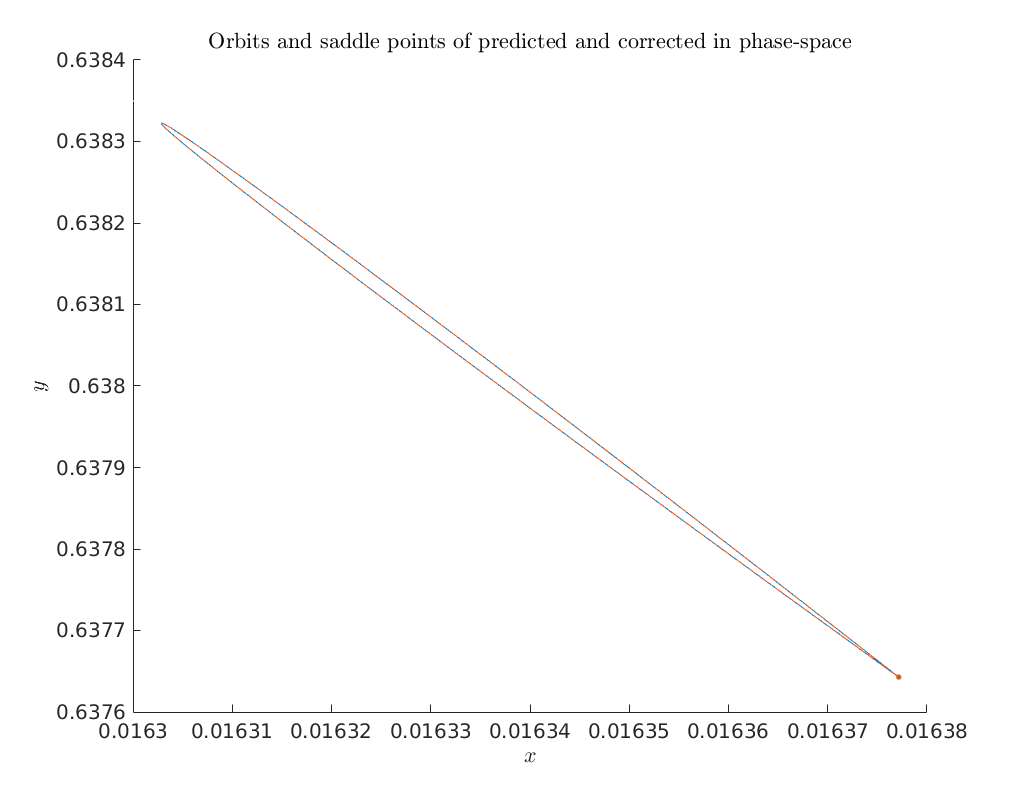
Compare predictor and corrected solution in \((x, y)\) phase-space¶

Below we compare the predicted and corrected homoclinic orbit in \((x, y)\) phase-space, as well as the predicted and corrected saddle point.

hold on
plot(x1_orbit(1:3:end),x1_orbit(2:3:end))
plot(homoclinic1_pred(1:3:end),homoclinic1_pred(2:3:end),'-.')
plot(x1_saddle(1), x1_saddle(2),'.', 'MarkerSize', 12, 'Color', [0 0.4470 0.7410])
plot(saddle1_pred(1), saddle1_pred(2),'.', 'MarkerSize', 12, 'Color', [0.8500, 0.3250, 0.0980])
xlabel('$x$')
ylabel('$y$')
title('Orbits and saddle points of predicted and corrected in phase-space')

Continue homoclinic curve emanating from Bogdanov-Takens point¶

Having obtain an initial approximation [hom_x, hom_v], where homo_v is the tangent vector to the homoclinic curve pointing outwards from the Bogdanov-Takens point, we can start continuation using the function cont. Since, we are not interested in bifurcations of the homoclinic orbit, we disable the detection of homoclinic bifurcations opt.Singularities = 0. This will reduce the computational cost. We also set the maximum number of continuation steps.

opt.Singularities = 0;
opt.MinStepsize  = 1e-06; 
opt.InitStepsize = 1e-03; 
opt.MaxStepsize  = 1e-02; 
opt.MaxNumPoints = 300;
homoclinic_br1 = cont(@homoclinic, hom1_x, hom1_v, opt);

first point found
tangent vector to first point found

elapsed time  = 13.6 secs
npoints curve = 300

Compare predicted with computed parameters emanating from bt1¶

Now that we have obtained a curve of homoclinic orbits (homoclinic_br) we compare the computed curve in parameter space with the predicted curve we construct below. To do so, we use the function BT_nmfm to obtain the parameter-dependent normal form coefficients and the coefficients between the parameters of the system and the parameters on the center manifold, see [Kuz21].

hold on
% plot computed parameter curve
plot(homoclinic_br1(homds.PeriodIdx+1,:), ...
     homoclinic_br1(homds.PeriodIdx+2,:));
% Bogdanov-Takens parameter-dependent normal form coefficients
bt1 = BT_nmfm_orbital(odefile, bt1, ap, BToptions);
a   = bt1.nmfm.a;
b   = bt1.nmfm.b;
K10 = bt1.nmfm.K10;
K01 = bt1.nmfm.K01;
K02 = bt1.nmfm.K02;
K11 = bt1.nmfm.K11;
K03 = bt1.nmfm.K03;
% construct predictor as in the paper
eps = linspace(0, 1.8);
beta1 = -4*a^3/b^4*eps.^4;
tau0  = 10/7;
tau2  = 288/2401;
beta2 = a/b*(tau0 + tau2*eps.^2).*eps.^2;
alpha = K10.*beta1 + K01.*beta2 + 1/2*K02.*beta2.^2 ...
    + K11.*beta1.*beta2 + 1/6*K03.*beta2.^3;
alpha = bt1.par(ap) + alpha;
% plot currect predictor
plot(alpha(1,:), alpha(2,:), '.')
% plot Bogdanov-Takens point
plot(bt1.par(ind.k2), bt1.par(ind.lambda), '.k', 'MarkerSize', 20)
% set axis labels and legend
xlabel('$k_2$')
ylabel('$\lambda$')
legend({'Homoclinic curve', 'Current homoclinic predictor', ...
    'Bogdanov-Takens point'}, 'Location', 'NorthWest')
title('Comparision between computed and predicted parameter curve.')

Center manifold coefficients' accuracy: 5.023537e-11

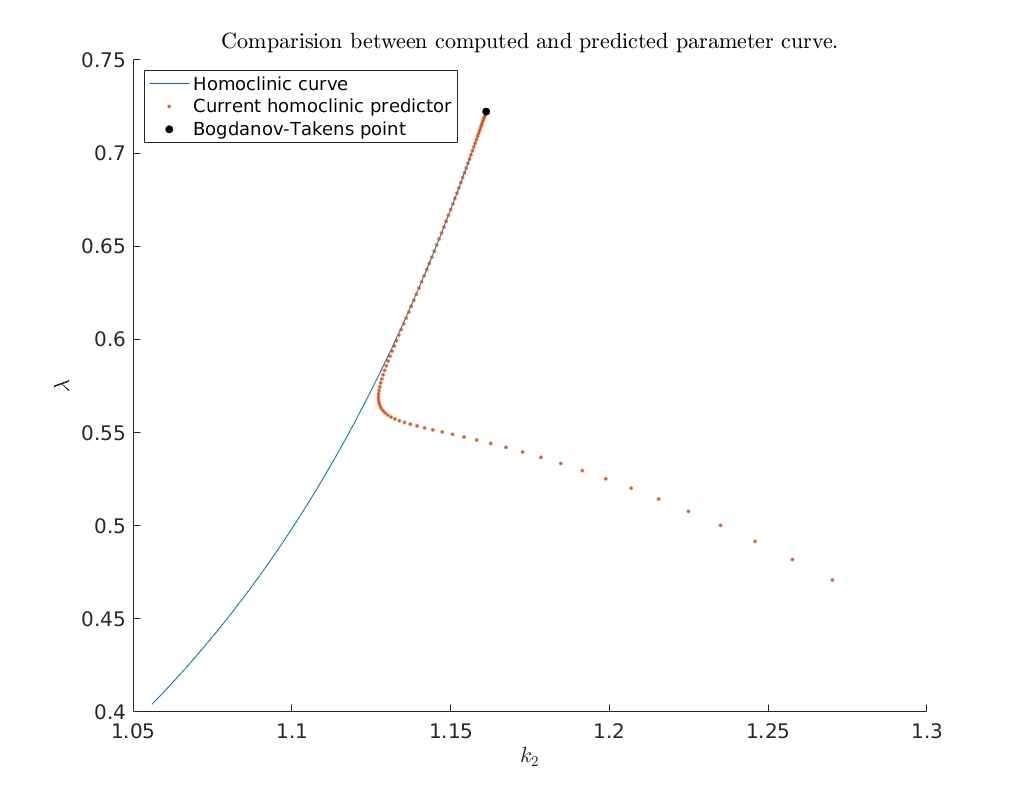
Bifurcation diagram in \((x,s)\) phase-space¶

To obtain an impression of the homoclinic solutions we plot the computed homoclinic orbits in \((x,s)\) phase-space.

hold on
%plot naive
plot(homoclinic_br1(homds.coords(1:homds.nphase:end), 1:10:end), ...
     homoclinic_br1(homds.coords(3:homds.nphase:end), 1:10:end), ...
     'Color', [0 0.4470 0.7410], 'HandleVisibility', 'Off')
xlabel('$x$')
ylabel('$s$')
plot(bt1.x(1), bt1.x(3), '.k' ,'MarkerSize', 20)
legend('Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(x,s)$-phase space')

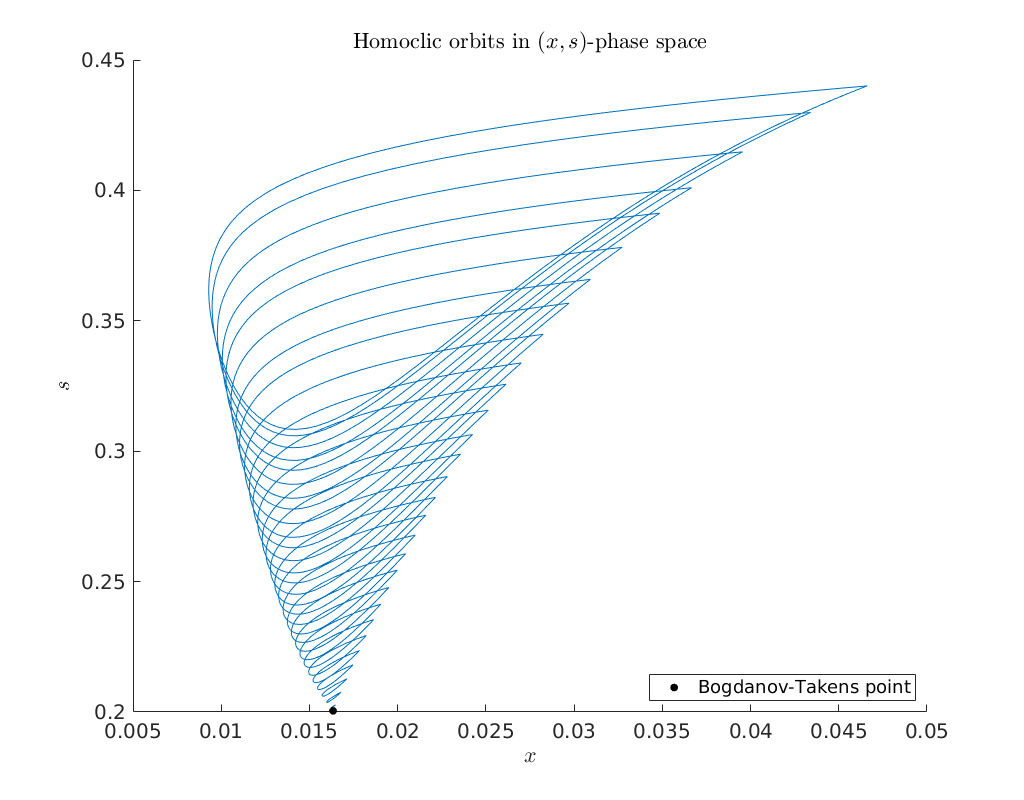
Continue homoclinic curve emanating from Bogdanov-Takens point¶

We continue the homoclinic orbit as usual with the MatCont function cont. However, since we already corrected the initial prediction to the homoclinic orbits, we use this correction as an initial starting point of continuation in stead of the predictor. If one isn’t interested in the correction of the initial point, the prediction could be used directly as argument to cont. Lastly, since, here, we are not interested in bifurcations of the homoclinic orbit, we disable the detection of homoclinic bifurcations. This will reduce the computational cost.

bt2_index = bt_points_info(2).index;
bt2.x = lp_br1(1:3, bt2_index);
bt2.par = p';
bt2.par(ap) = lp_br1(4:5, bt2_index);
options = BT_Hom_set_options();
[x2_pred, v2_pred] = init_BT_Hom(odefile, bt2,  ap, options);
homoclinic_br2 = cont(@homoclinic, x2_pred, v2_pred, opt);

Center manifold coefficients' accuracy: 2.761569e-11
BT normal form coefficients:
a=-8.378444e-02,	 b=-2.136280e+00
The initial perturbation parameter epsilon:  1.000000e-01
The initial amplitude: 0.00110154
The initial half-return time T: 1052.82
The initial distance eps0: 6.38083e-07
The initial distance eps1: 2.06064e-06
first point found
tangent vector to first point found

elapsed time  = 11.2 secs
npoints curve = 300

Continue Hopf point from the first Bogdanov-Takens point¶

We convert the first Bogdanov-Takens point into a Hopf point in order to start continuation of the Hopf bifurcation curve.

[hopf_x, hopf_v] = init_BT_H(odefile, bt1.x, bt1.par, ap);

We continue the Hopf point using the function cont. Then we try to filter out the neutral saddle points by inspecting the eigenvalues.

opt.MaxNumPoints = 2000;
opt.Singularities = 1;
opt.Eigenvalues = 1;
[hopf_br, ~, hopf_br_bif, ~, eigenvalues] = cont(@hopf, hopf_x, hopf_v, opt);
neutral_saddle_br = hopf_br(:,abs(imag(eigenvalues(2,:))) < 0.00001);
hopf_br_corrected = hopf_br(:,abs(imag(eigenvalues(2,:))) >= 0.00001);

first point found
tangent vector to first point found
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  2.031561e-16.
> In nf_H (line 27)
In hopf>testf (line 150)
In cont>EvalTestFunc (line 810)
In cont (line 506)

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  6.039544e-17.
> In nf_H (line 28)
In hopf>testf (line 150)
In cont>EvalTestFunc (line 810)
In cont (line 506)

label = BT, x = ( 0.016337 0.638410 0.200456 1.161199 0.722339 0.000000 )
(a,b)=(-4.822565e-02, -1.937633e+00)
label = BT, x = ( 0.115909 0.315467 0.288437 1.417628 0.971398 0.000000 )
(a,b)=(8.378444e-02, 2.136280e+00)
label = GH, x = ( 0.064311 0.211095 0.554870 0.924255 0.305879 0.003512 )
l2=-2.401234e+02
label = GH, x = ( 0.018022 0.368238 0.497968 0.891319 0.232487 0.003324 )
l2=-7.769003e+02
Closed curve detected at step 1241

elapsed time  = 1.3 secs
npoints curve = 1241

We see that in addition to the two Bogdanov-Takens points already detected before, there are also two generalized Hopf points (GH) detected.

Bifurcation diagram in phase-space \((x,s)\)¶

Below we plot the computed homoclinic orbits in \((x,s)\) phase-space.

hold on
colormap = lines();
homColor  = colormap(1,:);
hopfColor = colormap(2,:);
foldColor = colormap(5,:);
plot(homoclinic_br1(homds.coords(1:homds.nphase:end), 1:10:end), ...
     homoclinic_br1(homds.coords(3:homds.nphase:end), 1:10:end), ...
     'Color', homColor, 'HandleVisibility', 'Off')
plot(homoclinic_br2(homds.coords(1:homds.nphase:end), 1:10:end), ...
     homoclinic_br2(homds.coords(3:homds.nphase:end), 1:10:end), ...
     'Color', homColor, 'HandleVisibility', 'Off')
plot(lp_br1(1,:), lp_br1(3,:), 'Color', foldColor)
plot(hopf_br_corrected(1,:), hopf_br_corrected(3,:), 'Color', hopfColor)
plot(neutral_saddle_br(1,1:end-1), neutral_saddle_br(3,1:end-1), '--', ...
    'Color', hopfColor)
xlabel('$x$')
ylabel('$s$')
plot(bt1.x(1), bt1.x(3), '.k')
plot(bt2.x(1), bt2.x(3), '.k', 'HandleVisibility', 'Off')
legend('Limit point branch', 'Hopf branch', 'Neutral saddle branch', ...
    'Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(x,s)$-phase space')
axis([0 0.17 0 0.7])

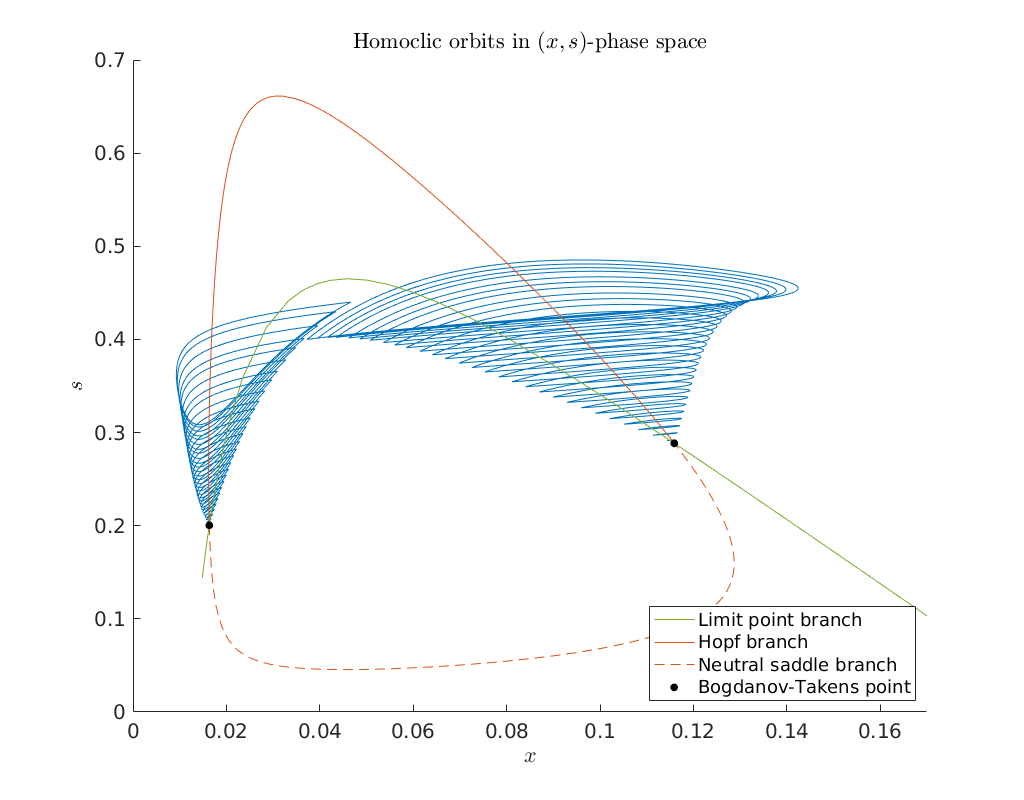
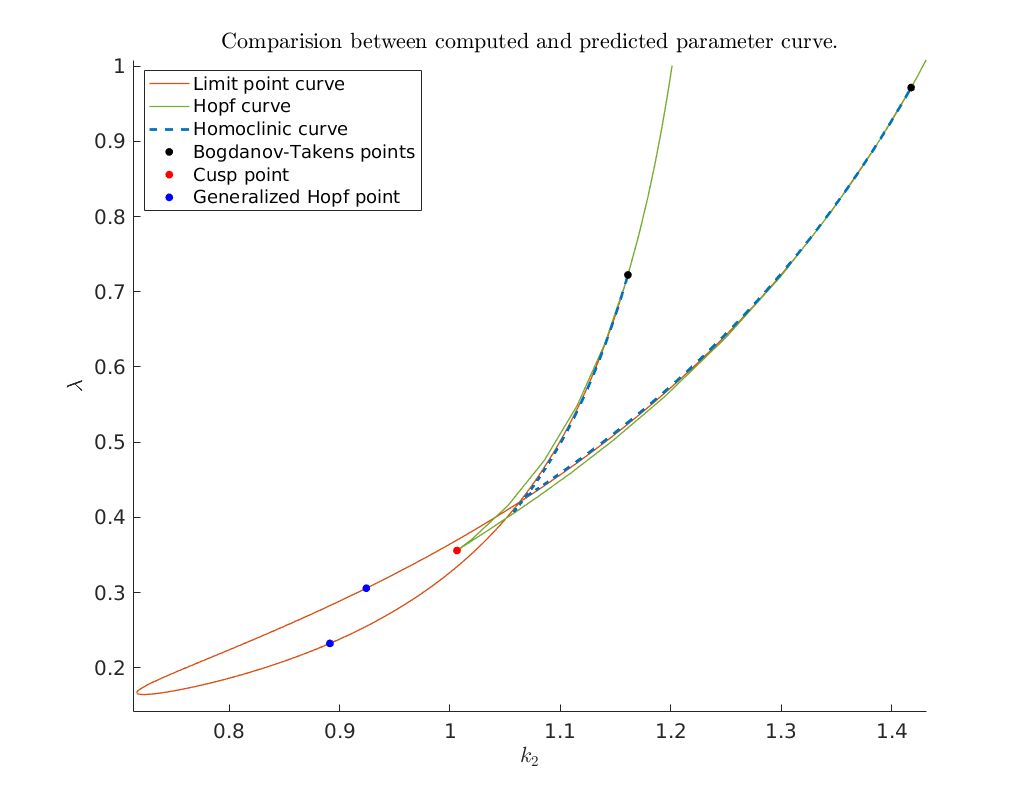
Bifurcation diagram in parameter-space \((k_2, \lambda)\)¶

We finish this notebook by plotting the computed homoclinic orbits in \((x,s)\) phase-space.

Below we extract the cusp bifurcation point and the generalized Hopf points on the limit point branch and Hopf branch respectively.

cusp_point_info = lp_br1_bif(strcmp({lp_br1_bif.label}, 'CP')==1);
genh_info = hopf_br_bif(strcmp({hopf_br_bif.label}, 'GH')==1);
cusp = lp_br1(:,cusp_point_info.index);
genh1 = hopf_br(:,genh_info(1).index);
genh2 = hopf_br(:,genh_info(2).index);

hold on
% plot computed parameter curve
plot(hopf_br_corrected(4,:), hopf_br_corrected(5,:), 'Color', hopfColor, 'linewidth', 1)
plot(lp_br1(4,:), lp_br1(5,:), 'Color', foldColor, 'linewidth', 1)
% plot homoclinic curves
plot(homoclinic_br1(homds.PeriodIdx+1,:), homoclinic_br1(homds.PeriodIdx+2,:), ...
     '--', 'Color', homColor, 'linewidth', 2)
plot(homoclinic_br2(homds.PeriodIdx+1,:), homoclinic_br2(homds.PeriodIdx+2,:), ...
     '--', 'Color', homColor, 'HandleVisibility', 'Off', 'linewidth', 2)
% plot Bogdanov-Takens point
plot(bt1.par(ind.k2), bt1.par(ind.lambda), '.k')
plot(bt2.par(ind.k2), bt2.par(ind.lambda), '.k', 'HandleVisibility', 'Off')
plot(cusp(4), cusp(5), '.r')
plot(genh1(4), genh1(5), '.b')
plot(genh2(4), genh2(5), '.b', 'HandleVisibility', 'Off')
% set axis, labels and legend
xlabel('$k_2$')
ylabel('$\lambda$')
legend({'Limit point curve', 'Hopf curve', 'Homoclinic curve', ... 
    'Bogdanov-Takens points', 'Cusp point', 'Generalized Hopf point'}, ...
    'Location', 'NorthWest')
title('Comparision between computed and predicted parameter curve.')
axis([0.7130    1.4320    0.1413    1.0081])

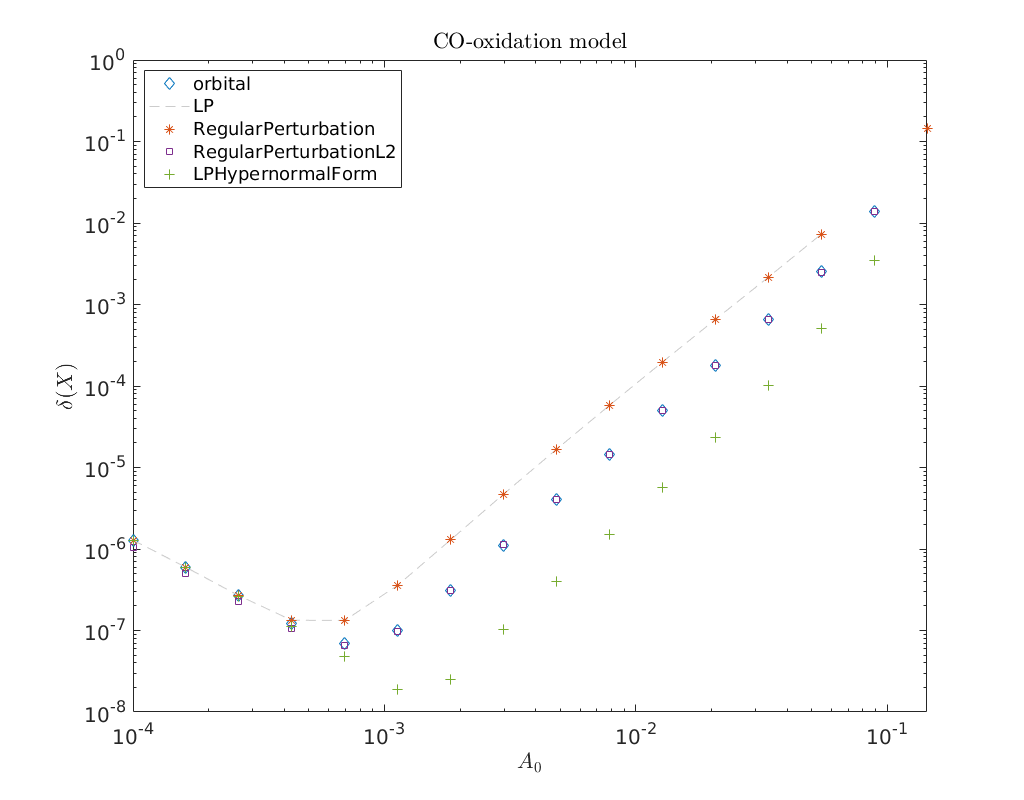
Convergence plot¶

We finish this notebook with a log-log convergence plot comparing the different third order homoclinic approximation methods derived in [Kuz21] to approximate the homoclinic solutions near the first Bogdanov-Takens point. On the abscissa is the amplitude \(A_0\) and on the ordinate the relative error \(\delta\) between the constructed solution (x_pred) to the defining system for the homoclinic orbit and the Newton corrected solution (x_corrected).

set(groot, 'defaultLineMarkerSize', 7);
options = BT_Hom_set_options();
options.TTolerance = 1e-05;
options.messages = false;
options.correct = false;

amplitudes = logspace(-4, 0, 20);
methodList = {'orbital', 'LP', 'RegularPerturbation', ...
    'RegularPerturbationL2', 'LPHypernormalForm'};
relativeErrors = {};
for i=1:length(methodList)
    options.method = methodList{i};
    relativeErrors{i} = zeros(size(amplitudes));
    for j=1:length(amplitudes)
    options.amplitude = amplitudes(j);
    [x_pred, v0] = init_BT_Hom(odefile, bt1, ap, options);
    try
        x_corrected = newtcorr(x_pred, v0);
        relativeErrors{i}(j) = norm(x_corrected-x_pred)/norm(x_corrected);
    catch
        warning('Did not converge.')
        continue
    end
  end
end

cm = lines();
loglog(amplitudes, relativeErrors{1}(:), 'd', ...
       amplitudes, relativeErrors{2}(:), '--', ...
       amplitudes, relativeErrors{3}(:), '*', ...
       amplitudes, relativeErrors{4}(:), 's', ...
       amplitudes, relativeErrors{5}(:), '+')
legend(methodList, 'Location', 'NorthWest')
title('CO-oxidation model')
xlabel('$A_0$')
ylabel('$\delta(X)$')
ax = gca;
ax.ColorOrder = [cm(1,:); [0.8 0.8 0.8]; cm(2,:); cm(4,:); cm(5,:)];

Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.

Interplay between normal forms and center manifold reduction for homoclinic predictors near Bogdanov-Takens bifurcation

CO-oxidation in a platinum model.¶

Overview¶

Load MatCont¶

Set the odefile¶

Define equilibrium¶

Continue equilibrium in parameter \(k_2\)¶

Construct limit point¶

Continue limit point in parameters \(k\) and \(T_m\)¶

Initial prediction of homoclinic orbit near Bogdanov-Takens point 1 (bt1)¶

Correct initial prediction of homoclinic orbit near bt1 with Newton¶

Compare profiles of predicted and corrected solution (bt1)¶

Compare predictor and corrected solution in \((x, y)\) phase-space¶

Continue homoclinic curve emanating from Bogdanov-Takens point¶

Compare predicted with computed parameters emanating from bt1¶

Bifurcation diagram in \((x,s)\) phase-space¶

Continue homoclinic curve emanating from Bogdanov-Takens point¶

Continue Hopf point from the first Bogdanov-Takens point¶

Bifurcation diagram in phase-space \((x,s)\)¶

Bifurcation diagram in parameter-space \((k_2, \lambda)\)¶

Convergence plot¶