.ipynb .pdf

repository open issue

Binder

Contents

Indirect field oriented control system

In [BR00, SGAR08] the following model is considered

(6)\[\begin{split}\begin{cases} \begin{aligned} \dot x_1 &= -c_1 x_1 + c_2 x_4 - \frac{k c_1}{u_2^0} x_2 x_4, \\ \dot x_2 &= -c_1 x_2 + c_2 u_2^0 + \frac{k c_1}{u_2^0} x_1 x_4, \\ \dot x_3 &= -c_3 x_3 - c_4 c_5 (x_2x_4 - u_2^0 x_1) + (c_4 T_m + c_3 w_{ref}), \\ \dot x_4 &= -(k_i-k_p)x_3 - k_p c_4 c_5 ( x_2 x_4 - u_2^0 x_1) + k_p (c_4 T_m + c_3 w_{ref}). \end{aligned} \end{cases}\end{split}\]

Here \(x_1 , x_2 , x_3\) and \(x_4\) are the state variables, where \(x_1\) and \(x_2\) represent, respectively, direct and quadrature components of the rotor flux; \(x_3\) is the rotor speed error; and \(x_4\) denotes the quadrature axis component of the stator current, respectively. We also define the following constants and parameters: \(u_2^0\) is a constant reference for the rotor flux magnitude; \(c_1\) to \(c_5\) are machine parameters; \(k_p\) and \(k_i\) are the proportional (P) and the integral (I) control gains, respectively; \(w_{ref}\) is the speed reference; \(T_m\) the load torque; \(k\) the measure of rotor time constant mismatches.

The parameters \(c_1,c_2,c_3,c_4,c_5,u_{20},k_p,k_i\) and \(w_{ref}\) are fixed as follows

\[\begin{split} \begin{aligned} c_1 &= 4.4868, \\ c_2 &= 0.3567, \\ c_3 &= 0, \\ c_4 &= 9.743, \\ c_5 &= 1.911, \\ u_2^0 &= 11.3, \\ k_p &= 4.5, \\ k_i &= 500, \\ w_{ref} &= 0, \\ \end{aligned} \end{split}\]

while the parameters \(k\) and \(T_m\) are used as unfolding parameters.

Overview

In this demo we will

• Define an analytically derived Bogdanov-Takens point.

• Start continuation of the homoclinic branch emanating from the Bogdanov-Takens points in two parameters \((k,T_m)\) using the new homoclinic smooth orbital predictor from [Kuz21].

• Compare the predicted and computed homoclinic bifurcation curve emanating from the Bogdanov-Takens point in parameters space.

• Compare a range of predictors for the homoclinic solutions emanating from the Bogdanov-Takens point with the corrected homoclinic solutions curve in phase-space.

• Create a convergence plot of the different homoclinic approximations derived in [Kuz21].

Load MatCont

Before we can start using MatCont we need to add the main directory of MatCont, as well as various subdirectories of MatCont, to the MATLAB search path. This is done in the code below. The variable matcont_home should point to the main directory of MatCont.

clear all
matcontpath = '../';
addpath(matcontpath)
addpath([matcontpath, 'Equilibrium'])
addpath([matcontpath, 'Systems'])
addpath([matcontpath, 'Hopf'])
addpath([matcontpath, 'Homoclinic'])
addpath([matcontpath, 'LimitPoint'])
addpath([matcontpath, 'LimitCycle'])
addpath([matcontpath, 'Continuer'])
addpath([matcontpath, 'MultilinearForms'])
addpath([matcontpath, 'Utilities'])
set(groot, 'defaultTextInterpreter', 'LaTeX');
set(0,'defaultAxesFontSize',15)

Set the odefile

Next we set the variable odefile to the system file previously generated by the notebook IFOCGenSym.ipynb.

odefile=@IFOC;

Define Bogdanov-Takens point manually

Since \(w_{ref}\) vanishes the equilibria of (6) are invariant under the transformation

(7)\[(x_1, x_2, x_3, x_4, T_m) \mapsto (-x_1, x_2, -x_3, -x_4, -T_m).\]

Then solving simultaneously for equilibria of (6) with vanishing determinant of the Jacobian with respect to the variables \(x_1, x_2, x_3\) and \(x_4\), and the unfolding parameter \(T_m\) yields four solutions. Two solutions are given by

\[\begin{split} \begin{aligned} x_1^{\pm} &= \frac{c_2 \left(k^2 \pm \sqrt{k^4-10 k^2+9}-1\right) |u_{20}|\sqrt{k^2 \mp \sqrt{k^4-10 k^2+9}-3}}{4 \sqrt{2} c_1 (k+1)|k|}, \\ x_2^{\pm} &= \frac{c_2 \left(\pm\sqrt{k^4-10 k^2+9}+k (k+4)+3\right) u_{20}}{4 c_1 k (k+1)}, \\ x_3 &= 0, \\ x_4^{\mp} &= -\frac{|u_{20}|\sqrt{\left(k^2\mp\sqrt{k^4-10 k^2+9}-3\right) }}{\sqrt{2}|k|}, \\ T_m^{\pm} &= -\frac{c_2 c_5 \left(k^2 \pm \sqrt{k^4-10 k^2+9}+3\right) u_{20} |u_{20}|\sqrt{k^2 \mp \sqrt{k^4-10 k^2+9}-3}}{4 \sqrt{2} c_1 k|k|}, \end{aligned} \end{split}\]

while the second two follow from the symmetry (7).

Next we solve for a double zero of the characteristic equation of the Jacobian with respect to the unfolding parameter \(k\). This reveals that there are two solutions given by

\[ (\pm x_1^-, x_2^-, 0, \pm x_4^+, \pm T_m^-), \]

with

\[ k = 1+\frac{1}{3} \sqrt[3]{216-24 \sqrt{57}}+\frac{2 \sqrt[3]{9+\sqrt{57}}}{3^{2/3}}. \]

Thus we can explicitly define the Bogdanov-Takens point

c1 = 4.4868;
c2 = 0.3567;
c5 = 1.911;
u20 = 11.3;
k = 1+(1/3)*(216+(-24)*57^(1/2))^(1/3)+2*3^(-2/3)*(9+57^(1/2))^(1/3);
x1m = (1/4)*2^(-1/2)*c1^(-1)*c2*(1+k)^(-1)*((-1)+k^2+(-1)*(9+( ...
      -10)*k^2+k^4)^(1/2))*(k^(-2)*((-3)+k^2+(9+(-10)*k^2+ ...
      k^4)^(1/2))*u20^2)^(1/2);
x2m = (1/4)*c1^(-1)*c2*k^(-1)*(1+k)^(-1)*(3+k*(4+k)+(-1)*(9+( ...
      -10)*k^2+k^4)^(1/2))*u20;
x3 = 0;
x4p = (-1)*2^(-1/2)*(k^(-2)*((-3)+k^2+(9+(-10)*k^2+k^4)^(1/2))*u20^2)^(1/2);
Tmm = (-1/4)*2^(-1/2)*c1^(-1)*c2*c5*k^(-1)*(3+k^2+(-1)*(9+( ...
      -10)*k^2+k^4)^(1/2))*u20*(k^(-2)*((-3)+k^2+(9+(-10)* ...
      k^2+k^4)^(1/2))*u20^2)^(1/2);
bt1.x = [x1m; x2m; x3; x4p];
bt1.par = [k; Tmm];

To refer to the parameters throughout the script we create a cell array of strings containing the parameter names. This is then converted into a struct. This allows us to refer to the parameters as ind.parametername, similar as done in DDE-BifTool.

parnames = {'k', 'Tm'};
cind = [parnames;num2cell(1:length(parnames))];
ind  = struct(cind{:});

Continue homoclinic curve emanating from the Bogdanov-Takens point

To continue the homoclinic curve emanating from the Bogdanov-Takens point we use the functions BT_Hom_set_options and init_BT_Hom to obtain an initial approximation to the homoclinic solution (hom_x) as well as a tangent vector to the discretized homoclinic solution (hom_v) as described in Initial prediction of homoclinic orbit near Bogdanov-Takens point 1.

ap = [ind.k, ind.Tm];
BToptions = BT_Hom_set_options();
[hom_x, hom_v] = init_BT_Hom(odefile, bt1,  ap, BToptions);
opt = contset;
opt.Singularities = 0;
opt.MaxNumPoints = 900;
homoclinic_br1 = cont(@homoclinic, hom_x, hom_v, opt);

BT normal form coefficients:
a=-2.800604e+01,	 b=9.109991e-01
The initial perturbation parameter epsilon:  1.000000e-01
The initial amplitude: 2.02473
The initial half-return time T: 1.17262
The initial distance time eps0: 0.0149101
The initial distance time eps1: 0.00705633
first point found
tangent vector to first point found

elapsed time  = 82.1 secs
npoints curve = 900

We see that the initial amplitude is large compared to the previously considered models. Nonetheless the homoclinic approximation converges and the homoclinic solution is continued correctly.

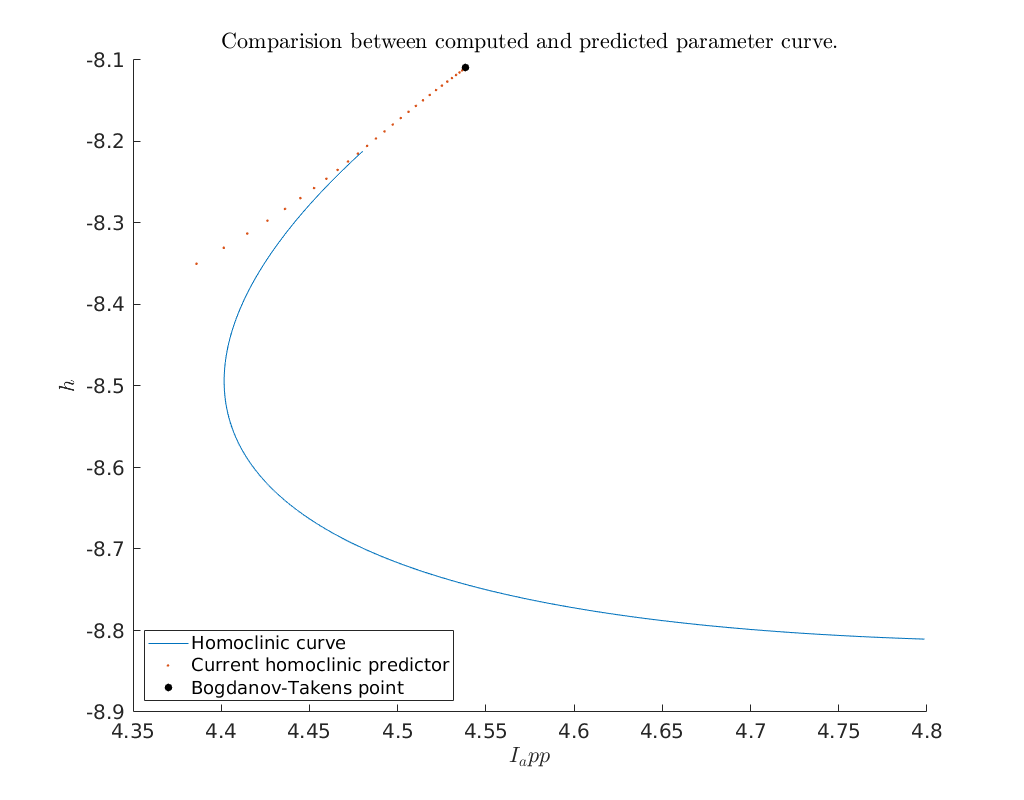
Compare predicted with computed parameters

Now that we have obtained a curve of homoclinic orbits (homoclinic_br) we compare the computed curve in parameter space with the predicted curve we construct below. To do so, we use the function BT_nmfm_orbital to obtain the smooth orbital normal form coefficients, i.e. \(a\) and \(b\), and the coefficients of the transformation \(K\) between the parameters of the system and the parameters of the smooth orbital normal form on the center manifold, see [Kuz21].

%plot --width 1024 --height 800
hold on
global homds
% plot computed parameter curve
plot(homoclinic_br1(homds.PeriodIdx+1,:), ...
     homoclinic_br1(homds.PeriodIdx+2,:));
% Bogdanov-Takens parameter-dependent normal form coefficients
bt1 = BT_nmfm_orbital(odefile, bt1, ap, BToptions);
a   = bt1.nmfm.a;
b   = bt1.nmfm.b;
K10 = bt1.nmfm.K10;
K01 = bt1.nmfm.K01;
K02 = bt1.nmfm.K02;
K11 = bt1.nmfm.K11;
K03 = bt1.nmfm.K03;
% construct predictor as in the paper
eps = linspace(0, 0.15, 30);
beta1 = -4*a^3/b^4*eps.^4;
tau0  = 10/7;
tau2  = 288/2401;
beta2 = a/b*(tau0 + tau2*eps.^2).*eps.^2;
alpha = K10.*beta1 + K01.*beta2 + 1/2*K02.*beta2.^2 ...
    + K11.*beta1.*beta2 + 1/6*K03.*beta2.^3;
alpha = bt1.par(ap) + alpha;
% plot currect predictor
plot(alpha(1,:), alpha(2,:), '.')
% plot Bogdanov-Takens point
plot(bt1.par(ind.k), bt1.par(ind.Tm), '.k', 'MarkerSize', 20)
% set axis labels and legend
xlabel('$I_app$')
ylabel('$h$')
legend({'Homoclinic curve', 'Current homoclinic predictor', ...
    'Bogdanov-Takens point'}, 'Location', 'SouthWest')
title('Comparision between computed and predicted parameter curve.')

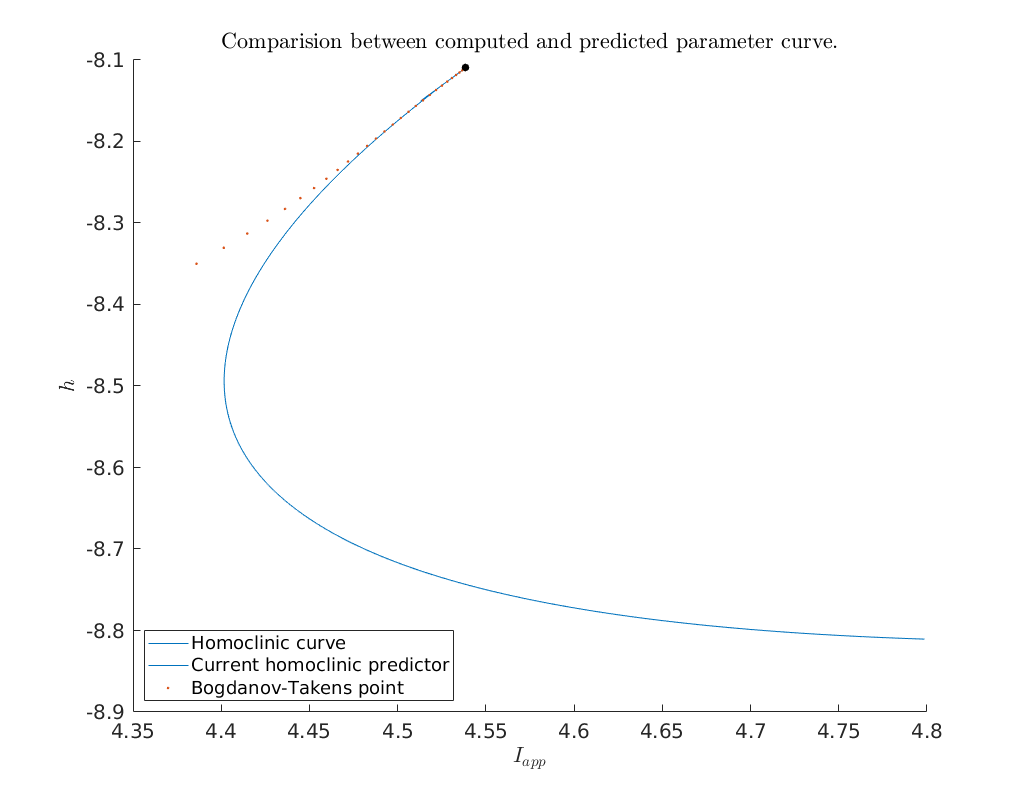
If we would like to have the homoclinic curve close to the Bogdanov-Takens point we could start the continuation of the homoclinic orbit with a smaller amplitude, for example with BToptions.amplitude = 0.1. Another possibility is to continue the homoclinic curve in the reverse direction. Here we choose the second approach.

[hom_x, hom_v] = init_BT_Hom(odefile, bt1,  ap, BToptions);
opt.Singularities = 0;
opt.MaxNumPoints = 120;
opt.Backward = 1;
homoclinic_br1_rev = cont(@homoclinic, hom_x, hom_v, opt);

BT normal form coefficients:
a=-2.800604e+01,	 b=9.109991e-01
The initial perturbation parameter epsilon:  1.000000e-01
The initial amplitude: 2.02473
The initial half-return time T: 1.17262
The initial distance time eps0: 0.0149101
The initial distance time eps1: 0.00705633
first point found
tangent vector to first point found
Current step size too small (point 97)
elapsed time  = 9.9 secs
npoints curve = 97

%plot --width 1024 --height 800
hold on
cm = lines();
homColor  = cm(1,:);
% plot computed parameter curve
plot(homoclinic_br1(homds.PeriodIdx+1,:), ...
     homoclinic_br1(homds.PeriodIdx+2,:), ...
     'Color', homColor);
plot(homoclinic_br1_rev(homds.PeriodIdx+1,:), ...
     homoclinic_br1_rev(homds.PeriodIdx+2,:), ...
     'Color', homColor);
% plot currect predictor
plot(alpha(1,:), alpha(2,:), '.', 'Color', cm(2,:))
% plot Bogdanov-Takens point
plot(bt1.par(ind.k), bt1.par(ind.Tm), '.k', 'MarkerSize', 20)
% set axis labels and legend
xlabel('$I_{app}$')
ylabel('$h$')
legend({'Homoclinic curve', 'Current homoclinic predictor', ...
    'Bogdanov-Takens point'}, 'Location', 'SouthWest')
title('Comparision between computed and predicted parameter curve.')

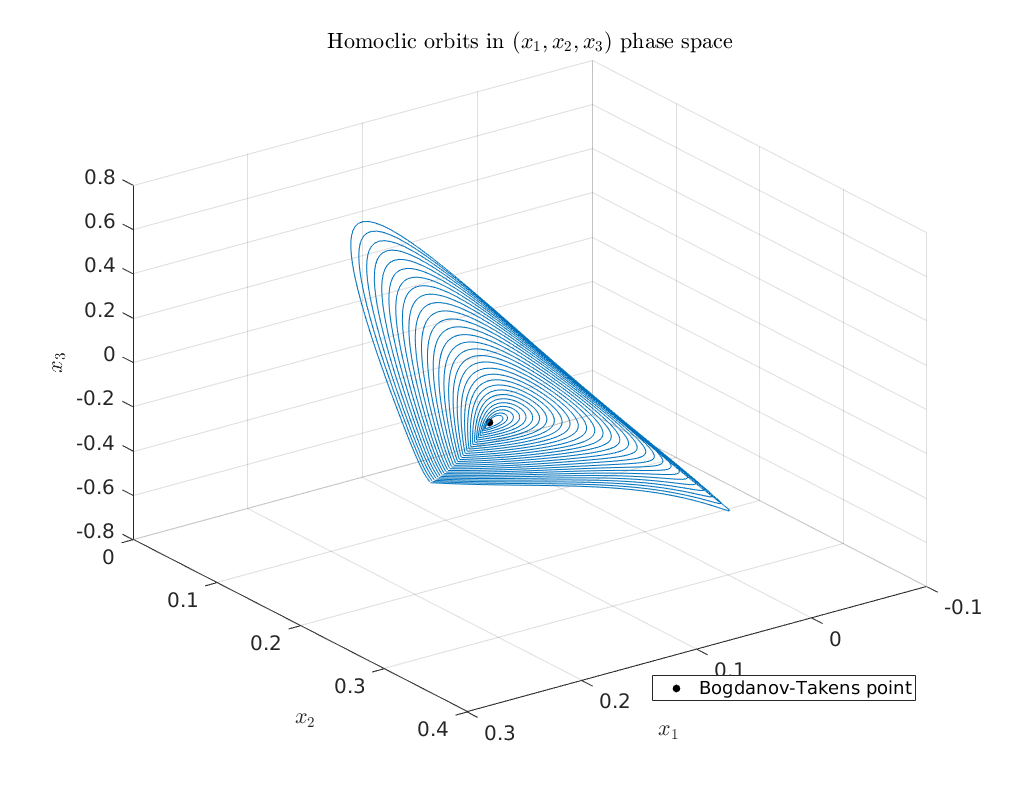
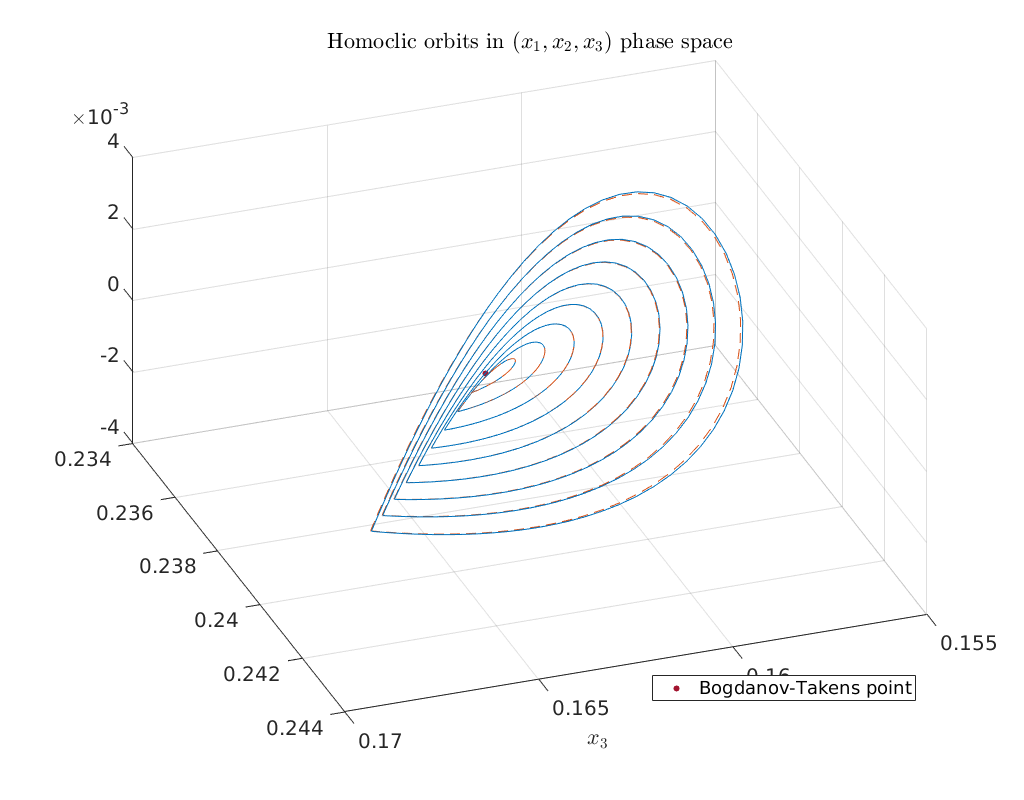
Plot of continued homoclinic solutions in \((x_1,x_2,x_3)\) phase-space

To obtain an impression of the homoclinic solutions we plot the computed homoclinic orbits in \((x_1,x_2,x_3)\) phase-space.

hold on
plot3(homoclinic_br1(homds.coords(1:homds.nphase:end), 1:30:end), ...
      homoclinic_br1(homds.coords(2:homds.nphase:end), 1:30:end), ...
      homoclinic_br1(homds.coords(3:homds.nphase:end), 1:30:end), ...
     'Color', [0 0.4470 0.7410], 'HandleVisibility', 'Off')
xlabel('$x_1$')
ylabel('$x_2$')
zlabel('$x_3$')
plot3(bt1.x(1), bt1.x(2), bt1.x(3), '.k' ,'MarkerSize', 20)
legend('Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(x_1,x_2,x_3)$ phase space')
grid on
view([144, 31]);

Predictors of orbits for various epsilons

Below we compute for a large range of amplitudes the predicted and corrected homoclinic solutions and compare them in phase space. We see that even with an amplitude of 1 the predicted homoclinic orbit is still very close.

options = BT_Hom_set_options();
options.messages = false;
options.correct = false;
options.TTolerance = 1.0e-05;

amplitudes = linspace(1.0e-03, 1, 10);
XPredicted = zeros(660,length(amplitudes));
XCorrected = zeros(660,length(amplitudes));
for j=1:length(amplitudes)
  options.amplitude = amplitudes(j);
  [x_pred, v0] = init_BT_Hom(odefile, bt1, ap, options);
  XPredicted(:,j) = x_pred;
  try
    XCorrected(:,j) = newtcorr(x_pred, v0);
  catch
    warning('Didn''t convergence to homoclinic solution')
  end
end

hold on
cm = lines;
plot3(XPredicted(homds.coords(1:homds.nphase:end),1:10), ...
      XPredicted(homds.coords(2:homds.nphase:end),1:10), ...
      XPredicted(homds.coords(3:homds.nphase:end),1:10), ...
      'color', cm(1,:), 'HandleVisibility', 'Off')
plot3(XCorrected(homds.coords(1:homds.nphase:end),1:10), ...
      XCorrected(homds.coords(2:homds.nphase:end),1:10), ...
      XCorrected(homds.coords(3:homds.nphase:end),1:10), ...
      '--', 'color', cm(2,:), 'HandleVisibility', 'Off')
plot3(bt1.x(1), bt1.x(2), bt1.x(3), '.', 'MarkerSize', 16)
legend('Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(x_1,x_2,x_3)$ phase space')
xlabel('$x_1$')
xlabel('$x_2$')
xlabel('$x_3$')
grid on
view([160, 45]);

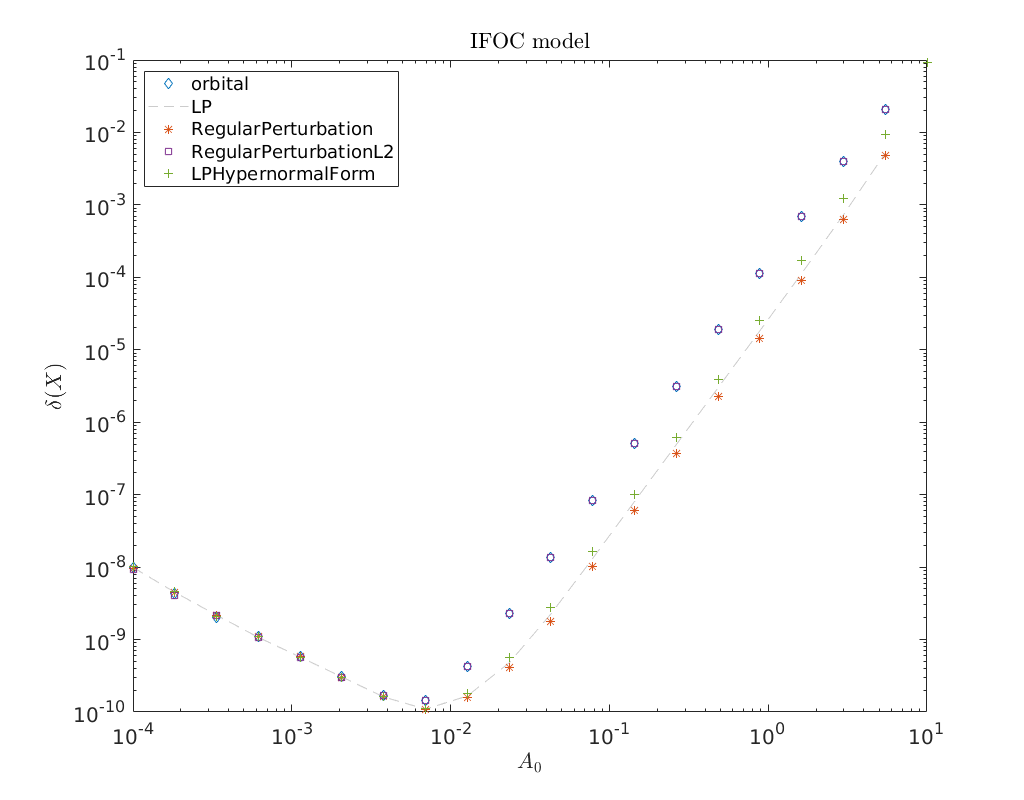
Convergence plot

We finish this notebook with a log-log convergence plot comparing the different third order homoclinic approximation methods derived in [Kuz21] to approximate the homoclinic solutions near the first Bogdanov-Takens point. On the abscissa is the amplitude \(A_0\) and on the ordinate the relative error \(\delta\) between the constructed solution (x_pred) to the defining system for the homoclinic orbit and the Newton corrected solution (x_corrected).

BToptions = BT_Hom_set_options();
BToptions.TTolerance = 1e-05;
BToptions.messages = false;
BToptions.correct = false;

amplitudes = logspace(-4, 1, 20);
methodList = {'orbital', 'LP', 'RegularPerturbation', ...
    'RegularPerturbationL2', 'LPHypernormalForm'};
relativeErrors = {};
for i=1:length(methodList)
    BToptions.method = methodList{i};
    relativeErrors{i} = zeros(size(amplitudes));
    for j=1:length(amplitudes)
    BToptions.amplitude = amplitudes(j);
    [x_pred, v0] = init_BT_Hom(odefile, bt1, ap, BToptions);
    try
        x_corrected = newtcorr(x_pred, v0);
        relativeErrors{i}(j) = norm(x_corrected-x_pred)/norm(x_corrected);
    catch
        warning('Did not converge.')
        continue
    end
  end
end

cm = lines();
loglog(amplitudes, relativeErrors{1}(:), 'd', ...
       amplitudes, relativeErrors{2}(:), '--', ...
       amplitudes, relativeErrors{3}(:), '*', ...
       amplitudes, relativeErrors{4}(:), 's', ...
       amplitudes, relativeErrors{5}(:), '+')
legend(methodList, 'Location', 'NorthWest')
title('IFOC model')
xlabel('$A_0$')
ylabel('$\delta(X)$')
ax = gca;
ax.ColorOrder = [cm(1,:); [0.8 0.8 0.8]; cm(2,:); cm(4,:); cm(5,:)];

Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.
Warning: Did not converge.

previous

Generate system files for the indirect field oriented control system

next

Generate system files for the extended Lorenz-84 model