Hodgkin Huxley equations¶

The Hodgkin-Huxley equations [HH52a] relate the difference in electric potential across the cell membrane \((V)\) and gating variables \((m, n\) and \(h\) ) for ion channels to the stimulus intensity \((I)\) and temperature \((T)\), as follows:

(9)¶\[\begin{split}\begin{cases} \begin{aligned} \dot{V} ={}& -G(V, m, n, h)+I, \\ \dot{m} ={}& \Phi(T)\left[(1-m) \alpha_{m}(V)-m \beta_{m}(V)\right], \\ \dot{n} ={}& \Phi(T)\left[(1-n) \alpha_{n}(V)-n \beta_{n}(V)\right], \\ \dot{h} ={}& \Phi(T)\left[(1-h) \alpha_{h}(V)-h \beta_{h}(V)\right], \end{aligned} \end{cases}\end{split}\]

where \(\dot{x}\) stands for \(\mathrm{d} x / \mathrm{d} t\) and \(\Phi\) is given by \(\Phi(T)=3^{(\mathrm{T}-6.3) / 10}\). The other functions involved are:

\[ G(V, m, n, h)=\bar{g}_{\mathrm{Na}} m^{3} h\left(V-\bar{V}_{\mathrm{Na}}\right)+\bar{g}_{\mathrm{K}} n^{4}\left(V-\bar{V}_{\mathrm{K}}\right)+\bar{g}_{\mathrm{L}}\left(V-\bar{V}_{\mathrm{L}}\right) \]

and the equations modeling the variation of membrane permeability are:

\[\begin{split} \begin{array}{ll} \alpha_{m}(V)=\Psi\left(\frac{V+25}{10}\right), & \beta_{m}(V)=4 e^{V / 18}, \\ \alpha_{n}(V)=0.1 \Psi\left(\frac{V+10}{10}\right), & \beta_{n}(V)=0.125 e^{V / 80} \\ \alpha_{h}(V)=0.07 e^{V / 20}, & \beta_{h}(V)=\left(1+e^{(V+30) / 10}\right)^{-1}, \end{array} \end{split}\]

with

\[\begin{split} \Psi(x) = \begin{cases} x /\left(e^{x}-1\right), & \text { if } x \neq 0, \\ 1, & \text { if } x=0. \end{cases} \end{split}\]

The parameters \(\bar{g}_{\text {ion }}\) and \(\bar{V}_{\text {ion }}\) representing maximum conductance and equilibrium potential for the ion were obtained from experimental data by Hodgkin and Huxley, with the values given below:

\[\begin{split} \begin{array}{lll} \bar{g}_{\mathrm{Na}}=120 \mathrm{mS} / \mathrm{cm}^{2}, & \bar{g}_{\mathrm{K}}=36 \mathrm{mS} / \mathrm{cm}^{2}, & \bar{g}_{\mathrm{L}}=0.3 \mathrm{mS} / \mathrm{cm}^{2}, \\ \bar{V}_{\mathrm{Na}}=-115 \mathrm{mV}, & \bar{V}_{\mathrm{K}}=12 \mathrm{mV}, & \bar{V}_{\mathrm{L}}=10.599 \mathrm{mV}. \end{array} \end{split}\]

The values of \(\bar{V}_{\mathrm{Na}}\) and \(\bar{V}_{\mathrm{K}}\) can be controlled experimentally [HH52b]. The temperature is set to \(T=6.3^{\circ}\).

Overview¶

In this demo we will

Manually define an Bogdanov-Takens point.
Start continuation of the homoclinic branch emanating from the Bogdanov-Takens points in two parameters \((\bar{V}_{\mathrm K},I)\) using the new homoclinic smooth orbital predictor from [Kuz21].
Compare the predicted and computed homoclinic bifurcation curve emanating from the Bogdanov-Takens point in parameters space.
Compare a range of predictors for the homoclinic solutions emanating from the Bogdanov-Takens point with the corrected homoclinic solutions curve in phase-space.
Create a convergence plot of the different homoclinic approximations derived in [Kuz21].

Load MatCont¶

Before we can start using MatCont we need to add the main directory of MatCont, as well as various subdirectories of MatCont, to the MATLAB search path. This is done in the code below. The variable matcont_home should point to the main directory of MatCont.

clear all
matcontpath = '../';
addpath(matcontpath)
addpath([matcontpath, 'Equilibrium'])
addpath([matcontpath, 'Systems'])
addpath([matcontpath, 'Hopf'])
addpath([matcontpath, 'Homoclinic'])
addpath([matcontpath, 'LimitPoint'])
addpath([matcontpath, 'LimitCycle'])
addpath([matcontpath, 'Continuer'])
addpath([matcontpath, 'MultilinearForms'])
addpath([matcontpath, 'Utilities'])
set(groot, 'defaultTextInterpreter', 'LaTeX');
set(0,'defaultAxesFontSize',15)

Set the odefile¶

Next we set the variable odefile to the system file previously generated by the notebook Generate system files for Hodgkin-Huxley equations.

odefile=@HodgkinHuxley;

Define Bogdanov-Takens point manually¶

By solving for real equilibria of (9) with double zero eigenvalues we obtain two equilibria. The first equilibrium is given by

\[ (V,m,n,h) = (-2.835463618170097, 0.07351498630356315, 0.361877602925177, 0.494859128785482), \]

with parameter values \(V_{\bar K} = (-4.977020454108788, -0.06185214966177632)\). The second solution we can discard, since the geometric multiplicity is equation to two.

To refer to the parameters throughout the script we create a cell array of strings containing the parameter names. This is then converted into a struct. This allows us to refer to the parameters as ind.parametername, similar as done in DDE-BifTool.

parnames = {'VbarK', 'I'};
cind = [parnames;num2cell(1:length(parnames))];
ind  = struct(cind{:});
ap = [ind.VbarK ind.I]; % continuation parameters

Next we define the Bogdanov-Takens point

V = -2.835463618170097;
m = 0.07351498630356315;
n = 0.361877602925177;
h = 0.494859128785482;
VbarK = -4.977020454108788;
I = -0.06185214966177632;
bt1.x = [V; m; n; h];
bt1.par = [VbarK; I];

Continue homoclinic curve emanating from the Bogdanov-Takens point¶

To continue the homoclinic curve emanating from the Bogdanov-Takens point we use the functions BT_Hom_set_options and init_BT_Hom to obtain an initial approximation to the homoclinic solution (hom_x) as well as a tangent vector to the discretized homoclinic solution (hom_v) as described in Initial prediction of homoclinic orbit near Bogdanov-Takens point 1.

ap = [ind.VbarK, ind.I];
BToptions = BT_Hom_set_options();
BToptions.ntst = 40;
[hom_x, hom_v] = init_BT_Hom(odefile, bt1,  ap, BToptions);
opt = contset;
opt.MaxNumPoints = 1000;
opt.Singularities = 0;
homoclinic_br1 = cont(@homoclinic, hom_x, hom_v, opt);

Center manifold coefficients' accuracy: 1.705303e-13
BT normal form coefficients:
a=2.551541e-05,	 b=-7.458949e-03
The initial perturbation parameter epsilon:  1.000000e-01
The initial amplitude: 0.0275168
The initial half-return time T: 12114.7
The initial distance eps0: 4.84346e-05
The initial distance eps1: 1.48445e-05
first point found
tangent vector to first point found

elapsed time  = 66.8 secs
npoints curve = 1000

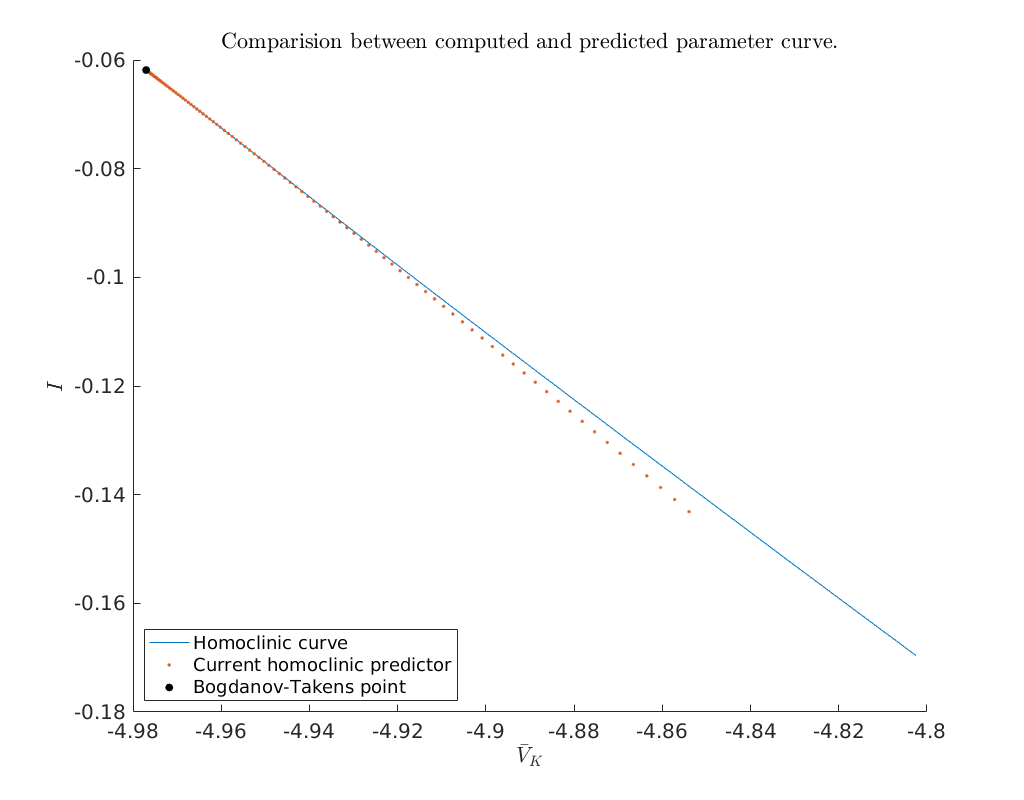
Compare predicted with computed parameters¶

Now that we have obtained a curve of homoclinic orbits (homoclinic_br) we compare the computed curve in parameter space with the predicted curve we construct below. To do so, we use the function BT_nmfm_orbital to obtain the smooth orbital normal form coefficients, i.e. \(a\) and \(b\), and the coefficients of the transformation \(K\) between the parameters of the system and the parameters of the smooth orbital normal form on the center manifold, see [Kuz21].

%plot --width 1024 --height 800
hold on
global homds
% plot computed parameter curve
plot(homoclinic_br1(homds.PeriodIdx+1,:), ...
     homoclinic_br1(homds.PeriodIdx+2,:));
% Bogdanov-Takens parameter-dependent normal form coefficients
bt1 = BT_nmfm_orbital(odefile, bt1, ap, BToptions);
a   = bt1.nmfm.a;
b   = bt1.nmfm.b;
K10 = bt1.nmfm.K10;
K01 = bt1.nmfm.K01;
K02 = bt1.nmfm.K02;
K11 = bt1.nmfm.K11;
K03 = bt1.nmfm.K03;
% construct predictor as in the paper
eps = linspace(0, 0.8);
beta1 = -4*a^3/b^4*eps.^4;
tau0  = 10/7;
tau2  = 288/2401;
beta2 = a/b*(tau0 + tau2*eps.^2).*eps.^2;
alpha = K10.*beta1 + K01.*beta2 + 1/2*K02.*beta2.^2 ...
    + K11.*beta1.*beta2 + 1/6*K03.*beta2.^3;
alpha = bt1.par(ap) + alpha;
% plot currect predictor
plot(alpha(1,:), alpha(2,:), '.')
% plot Bogdanov-Takens point
plot(bt1.par(ind.VbarK), bt1.par(ind.I), '.k', 'MarkerSize', 20)
% set axis labels and legend
xlabel('$\bar{V}_K$')
ylabel('$I$')
legend({'Homoclinic curve', 'Current homoclinic predictor', ...
    'Bogdanov-Takens point'}, 'Location', 'SouthWest')
title('Comparision between computed and predicted parameter curve.')

Center manifold coefficients' accuracy: 1.705303e-13

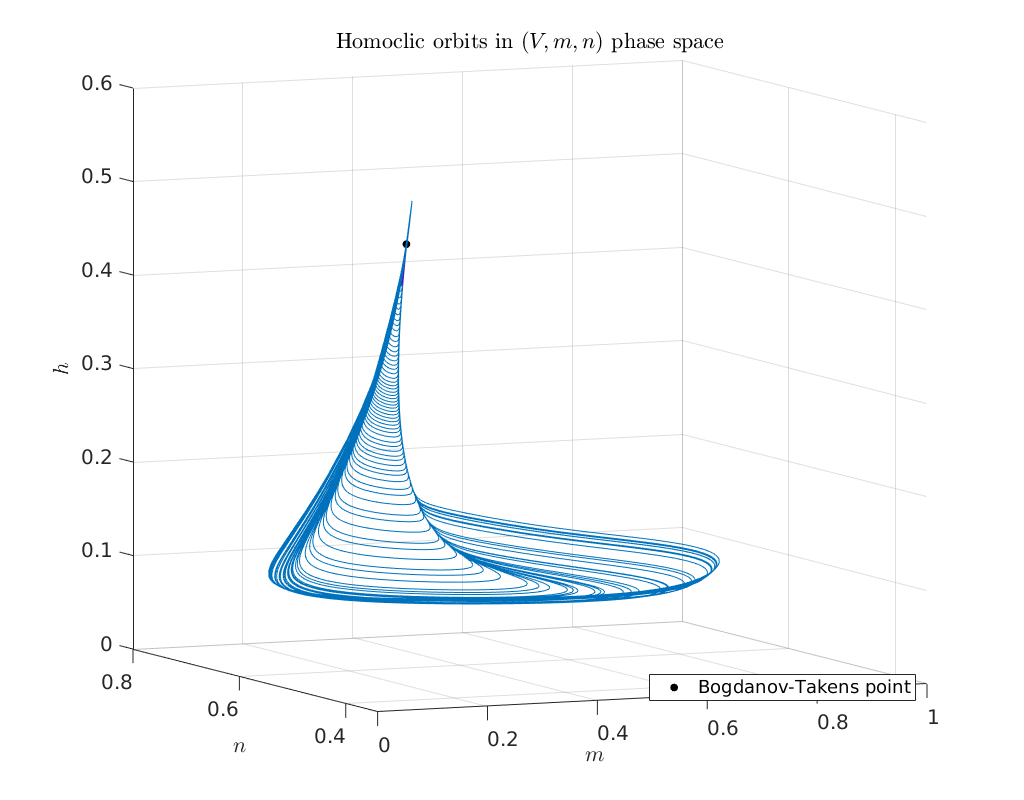
Plot of continued homoclinic solutions¶

To obtain an impression of the homoclinic solutions we plot the computed homoclinic orbits in \((m,n,h)\) phase-space.

%plot native
hold on
plot3(homoclinic_br1(homds.coords(2:homds.nphase:end), 1:60), ...
      homoclinic_br1(homds.coords(3:homds.nphase:end), 1:60), ...
      homoclinic_br1(homds.coords(4:homds.nphase:end), 1:60), ...
      'Color', [0 0.4470 0.7410], 'HandleVisibility', 'Off')
plot3(homoclinic_br1(homds.coords(2:homds.nphase:end), 61:100), ...
      homoclinic_br1(homds.coords(3:homds.nphase:end), 61:100), ...
      homoclinic_br1(homds.coords(4:homds.nphase:end), 61:100), ...
      'Color', [0.4470 0 0.7410], 'HandleVisibility', 'Off')
xlabel('$m$')
ylabel('$n$')
zlabel('$h$')
plot3(bt1.x(2), bt1.x(3), bt1.x(4), '.k' ,'MarkerSize', 20)
legend('Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(V,m,n)$ phase space')
grid on
view([-24, 7]);

%plot inline
hold on
plot3(homoclinic_br1(homds.coords(2:homds.nphase:end), 1:10:end), ...
      homoclinic_br1(homds.coords(3:homds.nphase:end), 1:10:end), ...
      homoclinic_br1(homds.coords(4:homds.nphase:end), 1:10:end), ...
      'Color', [0 0.4470 0.7410], 'HandleVisibility', 'Off')
xlabel('$m$')
ylabel('$n$')
zlabel('$h$')
plot3(bt1.x(2), bt1.x(3), bt1.x(4), '.k' ,'MarkerSize', 20)
legend('Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(V,m,n)$ phase space')
grid on
view([-24, 7]);

Predictors of orbits for various epsilons¶

Below we compute for a range of amplitudes the predicted and corrected homoclinic solutions and compare them in phase space. As seen from the plot above the homoclinic solutions start to deform rather quickly. Therefore, we cannot expect the approximation to be accurate for relative large amplitude values. Still, for an amplitude of \(0.3\) the approximation is nearby the corrected homoclinic solutions.

%plot native
options = BT_Hom_set_options();
options.messages = false;
options.correct = false;
options.TTolerance = 1.0e-05;

amplitudes = linspace(1.0e-02, 0.3, 5);
XPredicted = zeros(658,length(amplitudes));
XCorrected = zeros(658,length(amplitudes));
for j=1:length(amplitudes)
  options.amplitude = amplitudes(j);
  [x_pred, v0] = init_BT_Hom(odefile, bt1, ap, options);
  XPredicted(:,j) = x_pred;
  try
    XCorrected(:,j) = newtcorr(x_pred, v0);
  catch
    warning('Didn''t convergence to homoclinic solution')
  end
end

hold on
cm = lines;
plot3(XPredicted(homds.coords(2:homds.nphase:end),1:end), ...
      XPredicted(homds.coords(3:homds.nphase:end),1:end), ...
      XPredicted(homds.coords(4:homds.nphase:end),1:end), ...
      'color', cm(1,:), 'HandleVisibility', 'Off')
plot3(XCorrected(homds.coords(2:homds.nphase:end),1:end), ...
      XCorrected(homds.coords(3:homds.nphase:end),1:end), ...
      XCorrected(homds.coords(4:homds.nphase:end),1:end), ...
      '--', 'color', cm(2,:), 'HandleVisibility', 'Off')
plot3(bt1.x(2), bt1.x(3), bt1.x(4), '.', 'MarkerSize', 16)
legend('Bogdanov-Takens point', 'Location', 'SouthEast')
title('Homoclic orbits in $(X,Y,Z)$ phase space')
xlabel('$m$')
ylabel('$n$')
zlabel('$h$')
grid on
view([-24, 7]);

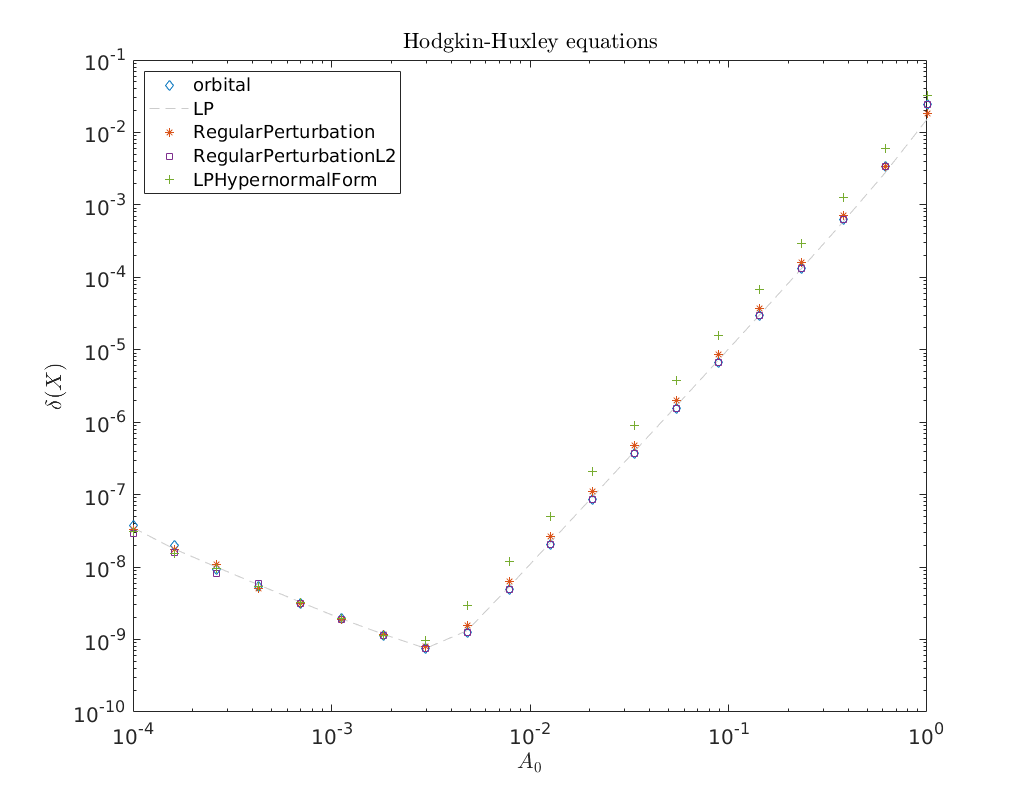
Convergence plot¶

We finish this notebook with a log-log convergence plot comparing the different third order homoclinic approximation methods derived in [Kuz21] to approximate the homoclinic solutions near the first Bogdanov-Takens point. On the abscissa is the amplitude \(A_0\) and on the ordinate the relative error \(\delta\) between the constructed solution (x_pred) to the defining system for the homoclinic orbit and the Newton corrected solution (x_corrected).

BToptions = BT_Hom_set_options();
BToptions.TTolerance = 1e-05;
BToptions.messages = false;
BToptions.correct = false;

amplitudes = logspace(-4, 0, 20);
methodList = {'orbital', 'LP', 'RegularPerturbation', ...
    'RegularPerturbationL2', 'LPHypernormalForm'};
relativeErrors = {};
for i=1:length(methodList)
    for o=1:3
        BToptions.method = methodList{i};
        BToptions.order = o;
        relativeErrors{o,i} = zeros(size(amplitudes));
        for j=1:length(amplitudes)
            BToptions.amplitude = amplitudes(j);
            [x_pred, v0] = init_BT_Hom(odefile, bt1, ap, BToptions);
            try
                x_corrected = newtcorr(x_pred, v0);
                relativeErrors{o,i}(j) = norm(x_corrected-x_pred)/norm(x_corrected);
            catch
                warning('Did not converge.')
                continue
            end
        end
    end
end

cm = lines();
loglog(amplitudes, relativeErrors{3,1}(:), 'd', ...
       amplitudes, relativeErrors{3,2}(:), '--', ...
       amplitudes, relativeErrors{3,3}(:), '*', ...
       amplitudes, relativeErrors{3,4}(:), 's', ...
       amplitudes, relativeErrors{3,5}(:), '+')
legend(methodList, 'Location', 'NorthWest')
title('Hodgkin-Huxley equations')
xlabel('$A_0$')
ylabel('$\delta(X)$')
ax = gca;
ax.ColorOrder = [cm(1,:); [0.8 0.8 0.8]; cm(2,:); cm(4,:); cm(5,:)];

Interplay between normal forms and center manifold reduction for homoclinic predictors near Bogdanov-Takens bifurcation